img

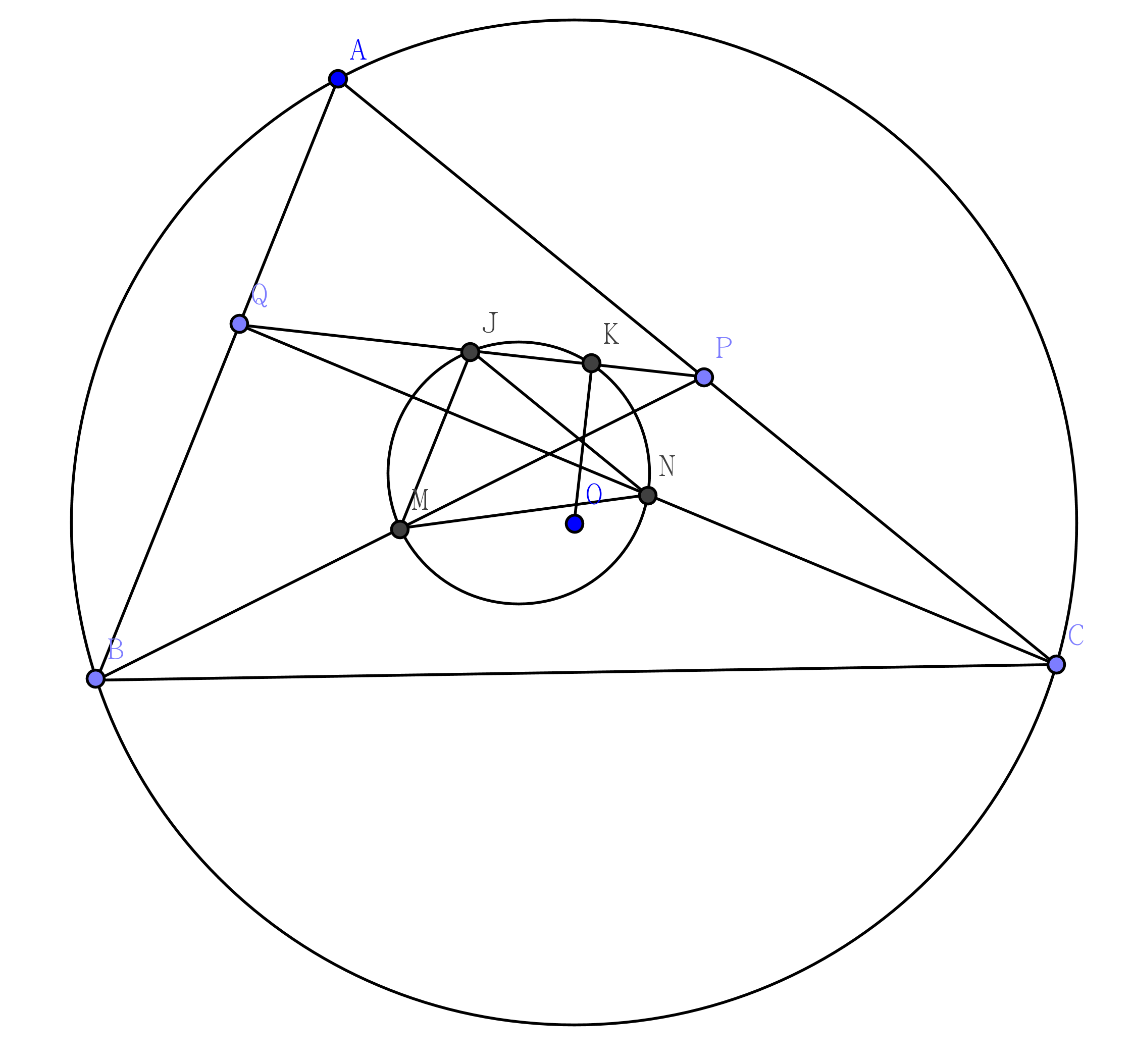
Problem

Let $ABC$ be a triangle and $(O)$ its circumcircle. $P \in AC,Q \in AB $. Let $M$ be the midpoint of $BP$, $N$ be the midpoint of $CQ$, $J$ be the midpoint of $PQ$. The circumcircle pass through $M N J$ meets $PQ$ at $K$. Prove: $OK \perp PQ$.

This problem is a generalization of the I.M.O. 2009 problem 2.
I found this problem at AoPS. And following two brief solutions are from there.

Solution 1

img

Let $H$ be the orthocenter of triangle $APQ$, $AE$ be a diameter of the circle $(O)$, and $IJ$ be a diameter of the circle $MNJ$. Suppose line $HQ$ meets line $EB$ at point $L$, and line $EC$ meets line $HP$ at point $R$.

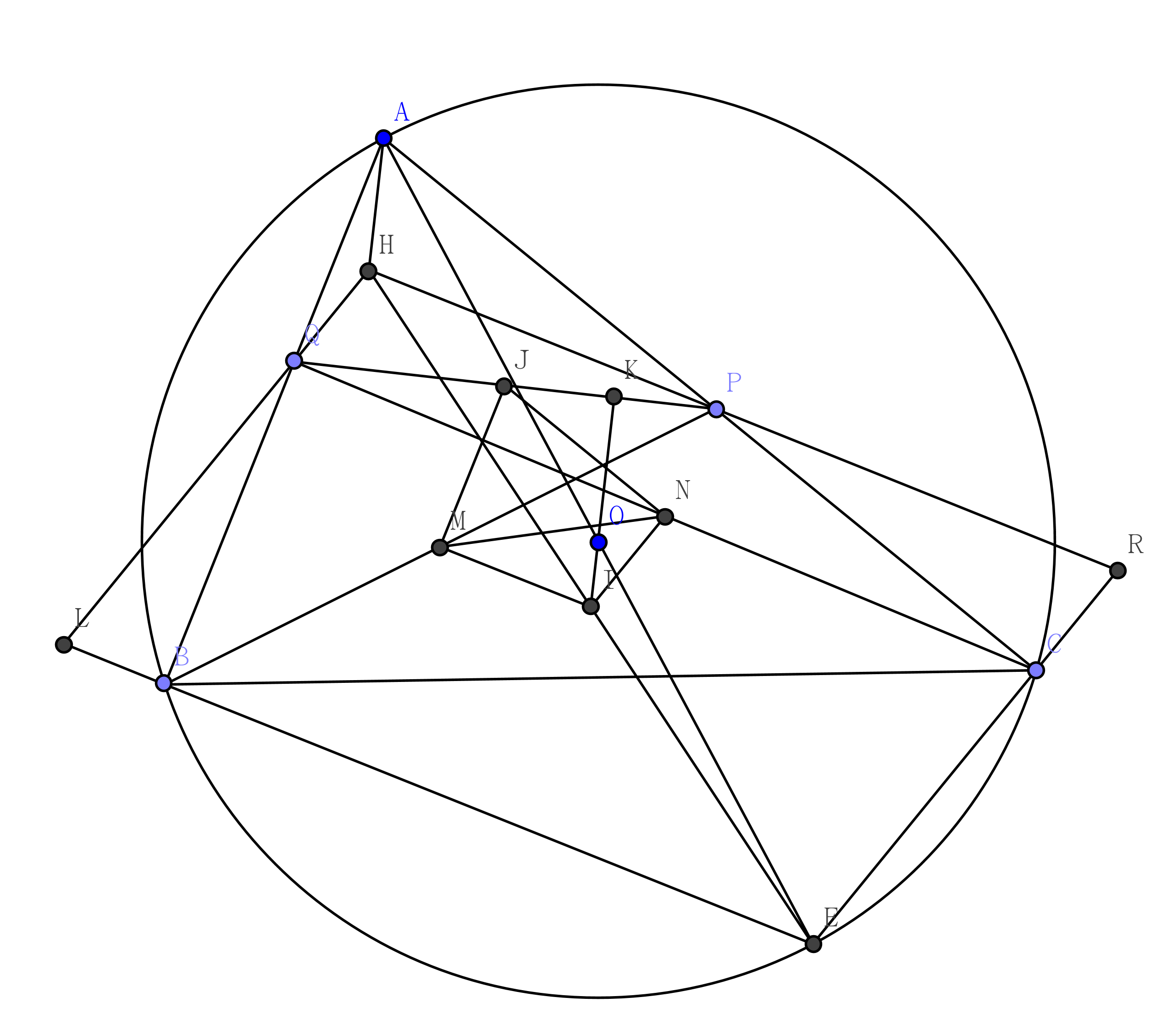
Since $HP \perp AB$, $EB \perp AB$, $MI \perp MJ$ and $MJ \parallel AB$, we know that $HP \parallel EB \parallel MI$. With Noting that $M$ is the midpoint of $BP$, the distance between line $MI$ and $HP$ is equal to the distance between line $MI$ and $EB$. A similar result also holds for $HQ, NI, EC$. Thus the point $I$ is the intersection point of the diagonals of the parallelogram $HLER$. Consequently, the point $I$ is the midpoint of $HE$ and $IO \parallel AH$. Finally, according to $AH \perp PQ$ and $IJ$ is a diameter, we have $IO \perp PQ$, $IK \perp PQ$.

Solution 2

img

Let $K’$ be the foot of the perpendicular line from $O$ to $PQ$, $BE \parallel MK’$, point $E$ be on the circle $(O)$. Suppose $BE$ meets $PQ$ at $X$ and $EC$ meets $QP$ at $Y$.

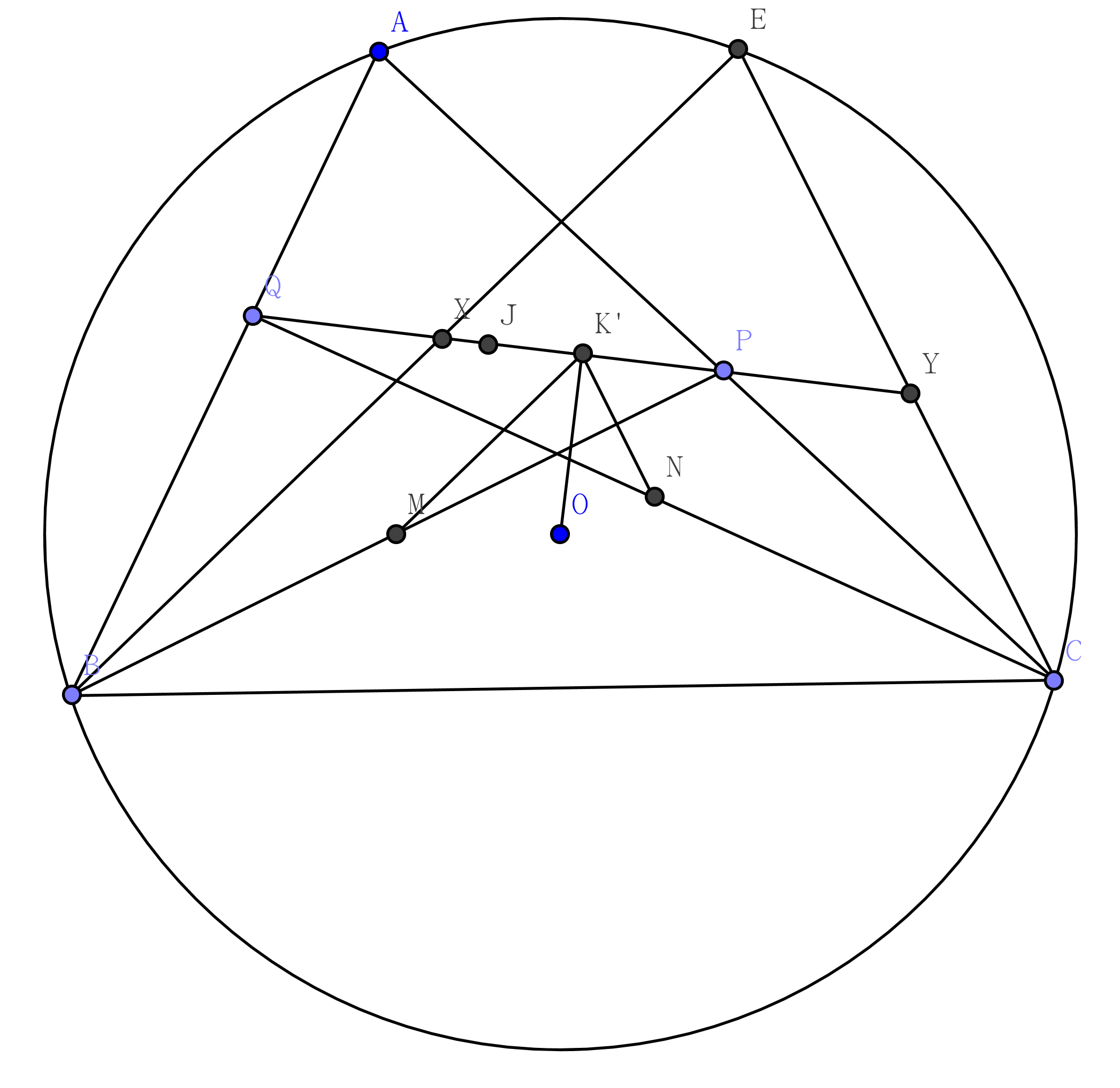
According to $M$ is the midpoint of $BP$ and $BX \parallel MK’$, $K’$ is the midpoint of $PX$. With applying Butterfly Theorem, we have $K’$ is the modpoint of $YQ$. So $NK’ \parallel CY$ and $\measuredangle NK’M = \measuredangle CEB = \measuredangle CAB = \measuredangle NJM$.

Reference