img

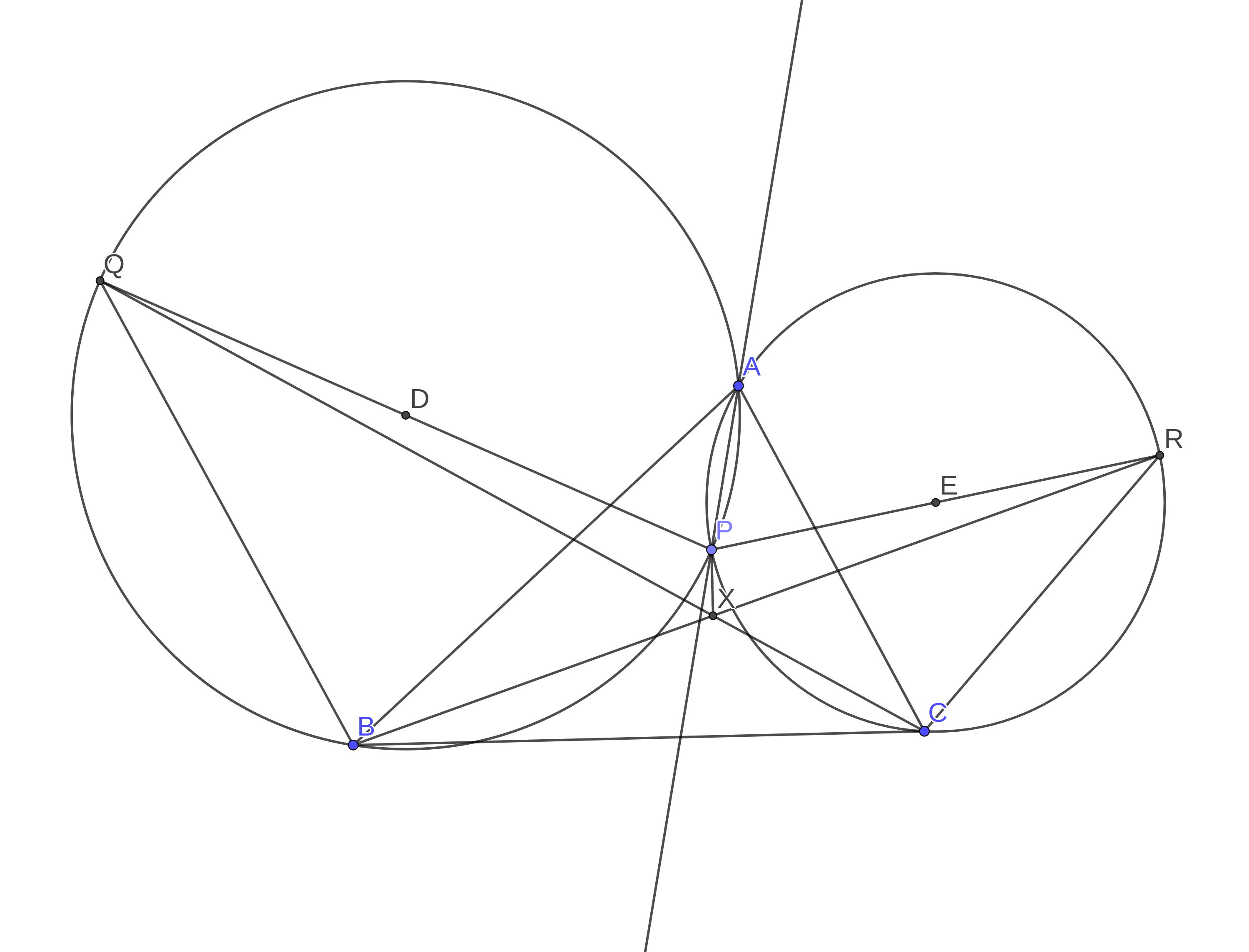
Problem

This problem is from The American Mathematical Monthly (problem 12092).

Let $ABC$ be a triangle, and let P be a point in the plane of the triangle satisfying $\angle BAP = \angle CAP$. Let $Q$ and $R$ be diametrically opposite $P$ on the circumcircles of $ABP$ and $ACP$, respectively. Let $X$ be the point of concurrency of line $BR$ and line $CQ$. Prove that $XP$ and $BC$ are perpendicular.

My solution

My solution is based on computation. Let $H$ be the foot of the perpendicular line from $P$ to $BC$. We just need to show that $XB^2 - XC^2 = BH^2 - CH^2$.

img

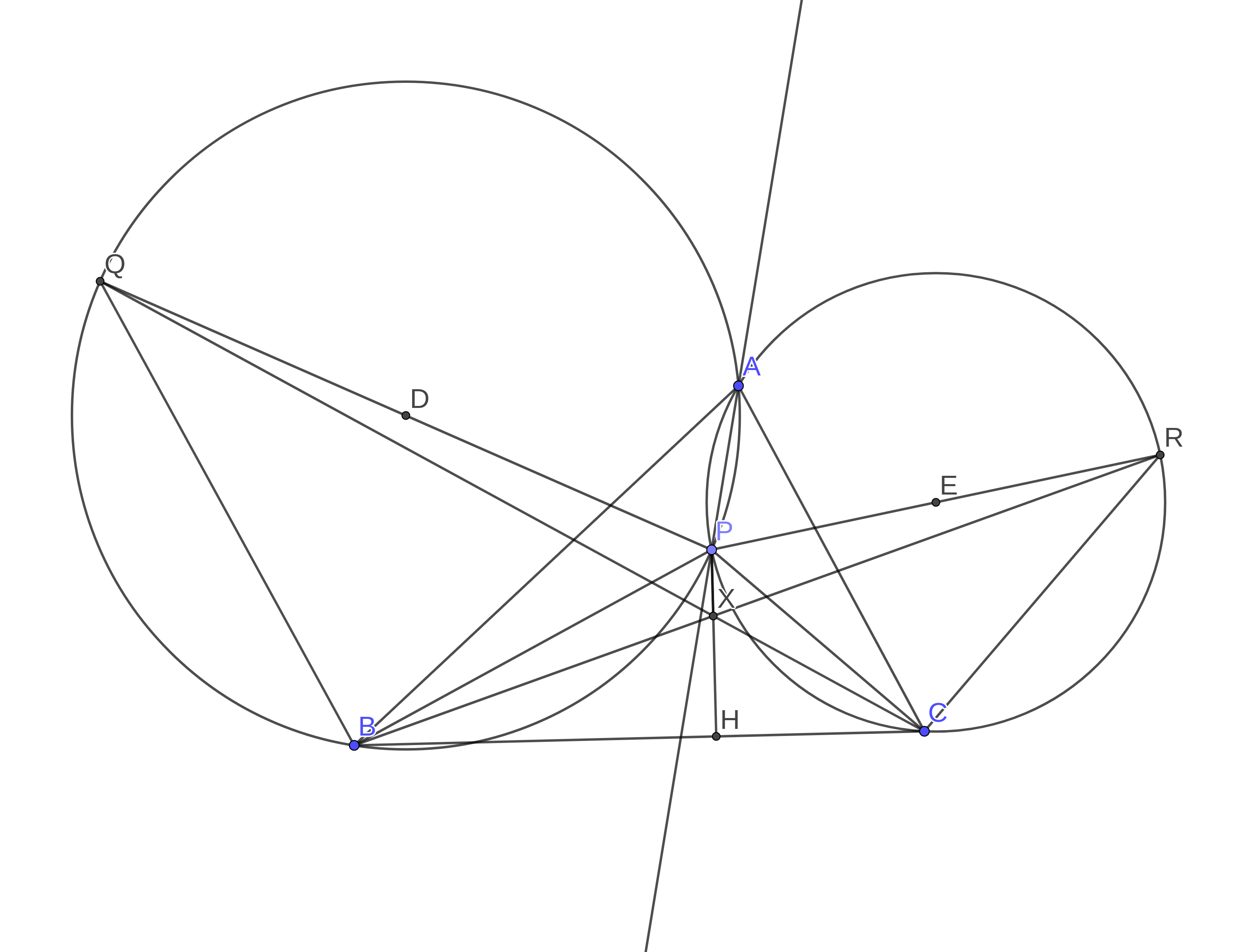
The area of Quadrilateral $RQBC$ is

$$\begin{align*} 2S_{RQBC} &= BC \cdot CR \sin \angle BCR + BC \cdot BQ \sin \angle CBQ + BQ \cdot CR \sin(\angle BCR + \angle CBQ) \\ &= BC \cdot CR \cos \angle PCB + BC \cdot BQ \cos \angle PBC + BQ \cdot CR \sin(\pi + \angle PBC + \angle PCB) \\ &= BC \left(\frac{PC\cos \angle PCB}{\tan A/2} + \frac{PB\cos \angle PBC}{\tan A/2}\right) + \frac{PB \cdot PC \sin\angle BPC}{\tan^2 A/2} \\ &= \frac{BC^2}{\tan A/2} + \frac{2 S_{PBC}}{\tan^2 A/2} = \frac{BC^2}{\tan A/2} + \frac{BC \cdot PH}{\tan^2 A/2} \\ & = \frac{BC}{\tan A/2} \left( BC + \frac{PH}{\tan A/2} \right), \end{align*}$$

where we use $\angle PBQ = \angle PCR = \pi / 2$ and $\angle PQB = \angle PRC = A / 2$ without explanation.

Hence we have

$$\begin{align*} BX &= \frac{S_{BCQ}}{S_{RQBC}} BR = \frac{BC \cdot BQ \sin \angle CBQ}{2S_{RQBC}} BR \\ &= \frac{BC \cdot PB \cos \angle PBC}{(2\tan A/2) S_{RQBC}} BR \\ &= \frac{BH \cdot BR}{BC + \frac{PH}{\tan A/2}}, \end{align*}$$

and similarly, $$CX = \frac{CH \cdot CQ}{BC + \frac{PH}{\tan A/2}}.$$

Note that

$$\begin{align*} &\quad~~ BH^2 BR^2 - CH^2 CQ^2 \\ &= BH^2 (BC^2 + CR^2 - 2 BC \cdot CR \cos \angle BCR ) - CH^2 (BC^2 + BQ^2 - 2BC \cdot BQ \cos \angle CBQ) \\ &= BC^2(BH^2 - CH^2) + \left(BH^2 \frac{PC^2}{\tan^2 A/2} - CH^2 \frac{PB^2}{\tan^2 A/2}\right) \\ &\quad + 2BH^2 BC \frac{PC \sin\angle PCB}{\tan A/2} - 2CH^2 BC \frac{PB \sin\angle PBC}{\tan A/2} \\ &= BC^2(BH^2 - CH^2) + \frac{BH^2(CH^2 + PH^2) - CH^2(BH^2 + PH^2)}{\tan^2 A/2} \\ &\quad + 2BH^2 BC \frac{PH}{\tan A/2} - 2CH^2 BC \frac{PH}{\tan A/2} \\ &= BC^2(BH^2 - CH^2) + \frac{PH^2(BH^2 - CH^2)}{\tan^2 A/2} + \frac{2BC \cdot PH}{\tan A/2} (BH^2 - CH^2) \\ &= (BH^2 - CH^2) \left(BC + \frac{PH}{\tan A/2}\right)^2, \end{align*}$$

i.e., $XB^2 - XC^2 = BH^2 - CH^2$.

Notes

  • With employing oriented area, angle and segment, this solution can be adopted for $P$ in a general position on the bisector of the angle $\angle BAC$.
  • We even never use the fact that $Q,A,R$ are collinear. It leads me to consider a better solution with beautiful geometric structure, however I have no idea so far.

Reference

  • Edited by Gerald A. Edgar, Daniel H. Ullman, Douglas B. West & with the collaboration of Paul Bracken (2019) Problems and Solutions, The American Mathematical Monthly, 126:2, 180-188, DOI: 10.1080/00029890.2019.1547601